

※決済画面でご記入いただいたメールアドレス宛にも本記事のURLを送付しています。本記事のURLはコピーするなどして紛失しないようにしてください。
SCOAの受検回数=100回以上・趣味はSCOAの受検。
日本で一番SCOAに詳しい、SCOAマスターのナオトです。
これを読めば、あなたはたった3時間の勉強でSCOAが通過できるようになるでしょう。
限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSCOA受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
SCOAを受検予定の人は知っておかないともったいないです。
✅ こんな人にオススメ
📌 SCOAを受検予定だが、対策に苦戦している人
📌 なんとしても内定を勝ち取りたい人
📌 SCOAの対策をする時間がとにかくない人
✅ 私の経歴・実績
私は早稲田大学に在籍しているとき、志望度の高い企業から内定を勝ち取るために早期から就活を始めました。
その企業ではSCOAの受検が必須で、高得点を取らないと足切りされてしまうことが事前にわかっていました。
なので、私はその企業に応募する前に、模試や志望度が低い企業にたくさん応募し、SCOAを100回以上受検して練習を重ねていきました。
※早稲田大学に在籍していた証拠として、卒業証明書を添付しておきます。

その経験を通して、私はSCOAの対策方法を熟知することができました。
日本で一番SCOAに詳しいのは間違いなく私であると自負しています。
そして、いつの間にかSCOAを受検することが趣味になり、今でも最新の情報を把握するため、定期的にSCOAを受検するようにしています。
さらには、本サイト(SCOA完全攻略サイト)を立ち上げ、SCOAに関する情報発信もするようにもなりました
私は自他ともに認める、完全なSCOAヲタクです。
それくらいSCOAに関しては誰にも負けない絶対的な自信と知識量があります。
※私の経験・知識をもとに高卒の友人にSCOAの指導をしたところ、短期間でかなり点数が伸びた(2割→7割)実績もあります。
以下はその友人からのお礼LINEです。
✅ この記事の内容
この記事の具体的な内容は以下です。
📌 前提知識:SCOAを受検するために必ず知っておくべきこと・心構え
📌 SCOAの点数を超短時間で伸ばす方法(科目別)
1万字超の史上最高傑作になっている自信があります。
私が過去100回以上ものSCOA受検を通して得た知見・テクニックをすべて詰め込んでいます。
時間をかけて本気で書き上げました。
✅ 販売実績・お客様の声
ありがたいことに、今まで500人以上のお客様にご購入いただきました。
感謝の声もたくさんいただいています(以下、一部ご紹介)

現在も購入者続出中のため、いつ値上げするかわかりません(今までに2回値上げしています)
今が最安値なので、購入を少しでも考えている人はお早めの購入をおすすめします。
無料部分はここまでです。では、一歩先で皆様をお待ちしています!
3時間の勉強でSCOAを通過し、内定に大きく近づきましょう。
——— ここから先が有料パート ———
※決済画面でご記入いただいたメールアドレス宛にも本記事のURLを送付しています。本記事のURLはコピーするなどして紛失しないようにしてください。
記事をご購入いただきありがとうございます。
ここからは私が100回以上ものSCOA受検を通して得た知識やテクニック、本には掲載されていない情報などをご紹介していきます。
※本記事はSCOAの通過や内定を保証するものではありません。
SCOAの前提知識
まず前提として、SCOAには
- SCOA-A
- SCOA-F
- SCOA-C
- SCOA-i
- SCOA-B
の4種類があります。
そして、出題される科目数によって上記4つはさらに
- SCOA-A(3尺度)
- SCOA-A(5尺度)
- SCOA-F(3尺度)
- SCOA-F(4尺度)
- SCOA-C
- SCOA-i
- SCOA-B
の7つに分けることができます。
※SCOAでは科目数を「尺度」で表します。例えば、出題される科目数が3科目の場合は3尺度となります。
上記7つそれぞれの出題科目と試験時間は以下の通りです。
| 種類 | 科目 | 試験時間 |
|---|---|---|
| SCOA-A(3尺度) | 言語、数理、論理 | 一括45分 |
| SCOA-A(5尺度) | 言語、数理、論理、英語、常識 | 一括60分 |
| SCOA-F(3尺度) | 言語、数理、論理 | 言語=20分、数理=15分、論理=15分 |
| SCOA-F(4尺度) | 言語、数理、論理、英語 | 言語=20分、数理=15分、論理=15分、英語=15分 |
| SCOA-C | 照合、分類、言語、計算、読図、記憶 | 各科目4分 |
| SCOA-i | 言語、数・論理、空間、知覚の正確さ | 一括20分 |
| SCOA-B | 性格検査 | 約35分 |
※詳しくは「SCOAは何問?100分で120問?SCOAの種類ごとに解説!」をご覧ください。
多くの企業はSCOA-A(5尺度 or 3尺度)+SCOA-B(性格検査)の組み合わせを導入しています。
なので、本記事ではSCOA-A(5尺度)の対策法について解説していきます。
※SCOA-B(性格検査)は用意された質問に直感で回答すれば良いだけなので、基本的に対策は不要です。よって、本記事では割愛させていただきます。
誤謬率について
SCOAでは誤謬率(ごびゅうりつ)が測定されません。
誤謬率とは回答数に対する不正解の割合のことです。
例えば100問の問題に回答し、不正解の数=30問の場合、誤謬率は30%となります。
誤謬率が計測される(=考慮される)テストの場合、問題を間違えるごとに点数に影響が出てしまいます。
なので、例えば全部で10問あるテストにおいて、
- A君=10問すべてに回答し、3問正解・7問不正解
- B君=10問中5問だけ回答し、2問正解・3問不正解(残り5問は未回答)
だった場合、正解数はA君の方が多いにも関わらず、点数はB君の方が高くなったりします。
つまり、誤謬率が計測されるテストではわからない問題は無理に回答しない方が良いということになります。
逆に、誤謬率が計測されないテストではわからない問題が登場しても勘で回答するのが得策ということになります。
SCOAでわからない問題が登場した場合は即座に勘で回答して次の問題に進むようにしてください。
SCOAはすべて選択式の問題なので、勘で回答しても正解する可能性が全然あります。
※「SCOAは全部埋めるべき?誤謬率は計測されない?される科目もあるのでご紹介します」もぜひ合わせてご覧ください。
言語の対策方法
言語は国語のことです。SCOAの言語の出題範囲は以下です。
- 言葉の意味(熟語・慣用句・故事成語など)
- 長文読解
SCOAの対策に時間があまり割けない人は、言語の対策は最悪しなくても良いです。
まず、言葉の意味は以下の例題のような知識問題なので、直前でなんとかなるものでもありません。
よって、時間が限られている中で言葉の意味の対策を行うのは得策ではありません。
【例題(熟語)】
次の熟語の読み方で、誤っているものはどれか。
- 化身(けしん)
- 必定(ひつじょう)
- 行灯(あんどん)
- 御利益(ごりやく)
- 脚立(きゃくたつ)
【解答&解説】
正解は5・・・(答)です。「脚立」は「きゃたつ」と読みます。
【例題(慣用句)】
次に示す言葉の意味で、正しいものを1〜5の中から選びなさい。
鼻であしらう
- 得意がって自慢すること
- 誇りに思うこと
- 他人に命令すること
- 出し抜いて人をあっと言わせること
- そっけない態度をとること
【解答&解説】
正解は5・・・(答)です。
長文読解は以下2つのポイントだけ頭に入れておいてください。
- 問題文を読む前に設問を読む
- 筆者が最も主張したいことは何かを意識しながら読む
まず1ですが、先に設問を読むと、問題文にどんな内容のことが書かれているのか少しは把握できますし、どこが・どのようなことが問題になっているかもつかめます。
2ですが、SCOAでは「問題文の主旨として最も妥当なものは、次のうちどれか」という問題が出題されるケースもあります。
筆者が最も主張したいことは何かを意識しながら読むことで以上の問題にも容易に対処できますし、「主たる内容」と「そうでないもの」とをはっきりと区別でき、文章全体の構成も容易に把握できます。
長文読解の例題も念のため掲載しておきます。
【例題】
次の文章を読んで後の質問に答えなさい。
ある哲学者が言っていた。もしわたしたちが言葉というものをもたなかったら、ひとはいまじぶんを襲っている感情がいったいどういうものか、おそらくは理解できなかったであろう、と。これが意味するところは、言葉が、何かすでにあるものを叙述するというより、なにかある、形のさだかでないものに、はじめてかたどりを与えるということだ。【ア】ということがあるということだ。
「分かる」とは、まさに言い得て妙である。もやもやしたこと、漠然としてなにか分からないものに包まれているとき、それをいくつかの要素に区分けする。たとえばひとの感情なら、喜怒アイ楽に分ける。いやそもそも感情じたいが意志や判断と分けてはじめて、それとして同定できるものである。形なきものに形を与えるということ、そこに言葉のはたらきがある。言葉にすることではじめて存在するようになるものがあるということだ。
いったん区分けをすると、こんどはそのはざまやあわいにあるものが見えてくる。陰りやグラテーションといった濃淡も見えてくる。さらにはその裏で同時にうごめきだしている反対感情も顕在化してくる。そのようにして、心にますますこまやかな起伏や襞が、【イ】「あや」(綾・彩)が生まれるのである。言葉が心にかたどりを与えるというのは、そういうことだ。
こうして言葉が心の機微を表わすようになる。が、これは、言葉が心をじゅうぶんに表現できないというのとじつは同じことである。ひとつの言葉でそれを表わしても、それにおさまりきらないものがかならずあるからである。言葉はひとつの切り取りであり、別の切り取り方をすれば、別の表情がそこに生まれるからである。
表すもの(言葉)とそれによって表されるもの(このばあいなら心や感情)との関係は、これほど動的であり、錯綜している。あるいは、レヴィ=ストロースの言葉を借りて、意味するものと意味されるものの関係は、つねに不均衡でありつづけると言ってもよい。
出典:鷲田清一『<想像>のレッスン』
(1)空欄アにあてはまる語句として、正しいものを1〜5の中から選びなさい。
- 言葉にしなくても分かる
- 言葉にしてはじめて分かる
- 言葉は明確な存在を補完する
- 感情は言葉で表現できない
- わたしたちは自分の感情が自分では理解できない
(2)下線部「言い得て妙である」理由として正しいものを1〜5の中から選びなさい。
- 「分かる」という言葉が「分かる」過程を現しているから
- もやもやしたことが「分かる」過程が巧妙であるから
- 漠然とした何か分からないものを言葉が明確にしてくれるから
- 感情は、意志や判断と分けることではじめて固定できるから
- 「分かる」という過程に言葉が重要な役割を果たしているから
(3)下線部「喜怒アイ楽」のカタカナを漢字で書いたものとして正しいものを1〜5の中から選びなさい。
- 会
- 相
- 合
- 愛
- 哀
(4)空欄イにあてはまる語句として、正しいものを1〜5の中から選びなさい。
- だが
- そのため
- なぜなら
- つまりは
- だから
(5)下線部「意味するものと意味されるものの関係は、つねに不均衡でありつづける」が意味していることとして正しいものを1〜5の中から選びなさい。
- 言葉で意味されることは、つねに錯綜している。
- 言葉で意味することは、つねに不十分である。
- 意味されるものはつねに意味するものより不足している。
- 意味するものと意味されるものとはつねに入れ替わる。
- 言葉の数は意味されるものより少ない。
【解答&解説】
(1)正解は2・・・(答)です。空欄を含む第1段落の後半の文章は、前半の言い換えとなっており、さらに空欄の前文では、言葉の定義をしているので、「言葉にしてはじめて分かる」が妥当です。
(2)正解は1・・・(答)です。言い得て妙であるとは、巧に言い表しているさまを意味します。「分かる」という言葉が、何を巧に言い表しているのかといえば、人が「分かる」という過程が、文字通り、「分ける」作業を伴うということが述べられています。
(3)正解は5・・・(答)です。
(4)正解は4・・・(答)です。空欄の前の文章を、空欄の後の文章で言い換えているので、「つまりは」が正しいです。
(5)正解は2・・・(答)です。「意味するものと意味されるものの関係は、つねに不均衡でありつづける」の不均衡に該当する説明があるものは選択肢2・3・5です。
ここで「意味するものと意味されるもの」はその前文に対応しているので、「意味するもの=意味を付与するもの=言葉」と「意味されるもの=意味を付与されるもの=心や感情」です。
したがって、2が正しいことがわかります。3は心や感情は常に言葉より不足している、と読み替えられるので誤りです。5は言葉の数を問題にしているのではないので誤りです。
SCOAの言語では言葉の意味に時間をかけず、どれだけ長文読解に時間を使えるかが勝負です。
言葉の意味でわからない問題が出題された場合は即座に勘で回答して次の問題に進んでください。
知識問題は知ってるか・知らないかの二択なので、ウダウダ悩むのは時間の無駄です。
※「SCOAの言語を完全解説!問題例・対策方法は?」もぜひ合わせてご覧ください。
数理の対策方法
数理は数学のことです。
SCOAの受検までに時間がない人は数理と、この後ご紹介する論理にできるだけ勉強の時間を割いてください。
SCOAの数理の出題範囲は以下です。
- 四則計算
- 一次方程式
- 二次方程式
- 不等式
- 数列
- 数的推理
それぞれについて詳しく解説していきます。
四則計算
四則計算は以下のような計算問題です。
【例題】
次の計算をしなさい。
3×4÷(5+6)÷7
- 1/7
- 3/7
- 5/7
- 12/77
- 16/77
【解答&解説】
3×4÷(5+6)÷7=12÷11÷7=12/11 ÷ 7=12/77・・・(答)となります。
ほとんどの人にとっては特段の対策は不要でしょう。
本番では「ミスなく・正確に」を意識しながら解く以外に意識することはありません。
一次方程式
こちらもほとんどの人にとっては特段の対策は不要です。
以下のような問題が出題されます。
【例題】
次の式を解きなさい。
3(3x-1)-4(x-2)=12
- x=-7/5
- x=7/12
- x=1/6
- x=7/5
- x=-17/12
【解答&解説】
3(3x-1)-4(x-2)=12
⇔ 9x-3-4x+8=12
⇔ 5x+5=12
⇔ 5x=7
⇔ x=7/5・・・(答)となります。
一次方程式の解き方を忘れてしまった人は必ず思い出しておいてください。
一次方程式の解き方はGoogleやYahoo!で「一次方程式 解き方」などと検索すればいくらでも出てくるので、本記事では割愛します。
二次方程式
二次方程式の解き方は忘れてしまった人も多いのではないでしょうか。
SCOAの二次方程式では以下のような問題が出題されます。
次の式を解きなさい。
x2-3x-18=0
- x=3、-6
- x=6、-3
- x=3、6
- x=-6、-3
- x=9、-3
【解答&解説】
x2-3x-18=(x+3)(x-6)より、x=6、-3・・・(答)です。
二次方程式は因数分解を使うと簡単に解ける場合が多いですが、SCOAの受検までに時間がなく、因数分解のやり方を忘れてしまった・因数分解が苦手な人は「解の公式」を覚えてください。
解の公式は以下です。

上記の例題を解の公式で解いてみます。
まず、x2-3x-18=0より、
- a=1
- b=-3
- c=-18
です。よって、
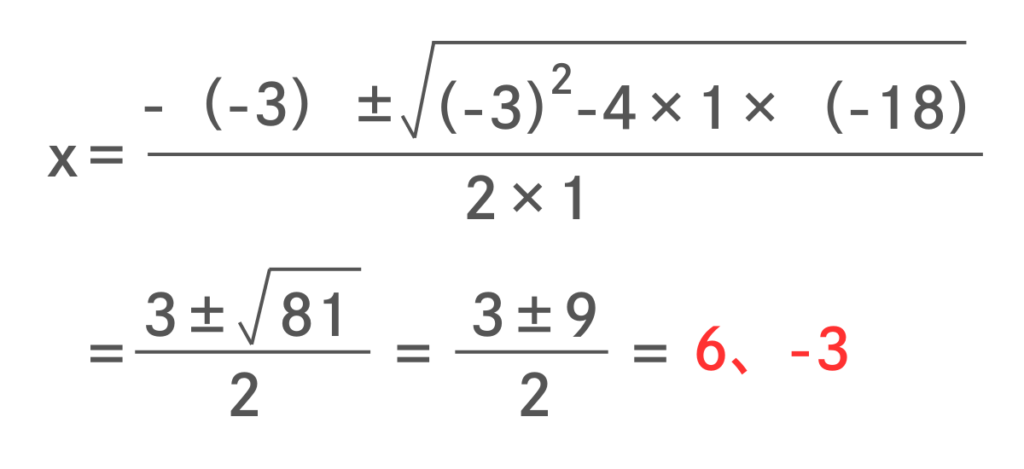
となります。
因数分解が苦手な人は解の公式を使って計算するようにしてください。
二次方程式の解き方は一次方程式と同様に、GoogleやYahoo!で「二次方程式 解き方」などと検索すればいくらでも出てくるので、本記事では割愛します。
不等式
SCOAの不等式では以下のような問題が出題されます。
【例題】
次の不等式を解きなさい。
2(x-4)+5<3x-4
- x<2
- x>1
- x>2
- x<4
- x>5
【解答&解説】
2(x-4)+5<3x-4
⇔ 2x-8+5<3x-4
⇔ 2x-3<3x-4
⇔ -x<-1
⇔ x>1・・・(答)となります。
不等式も多くの人にとっては特段の対策は不要でしょう。
不等式ではマイナスの掛け算、割り算による不等号の向きの変化にご注意ください。
上記の例題では、-x<-1の両辺にマイナス1を掛け算することでx>1になり、不等号の向きが逆になっています。
数列
SCOAを受検予定の多くの人が対策すべき数理の問題は、数列とこの後ご紹介する数的推理です。
上記でご紹介した
- 四則逆算
- 一次方程式
- 二次方程式
- 不等式
は解の公式を除けば解き方を覚えている人も多いと思いますので、それに該当する人はサクッと見直して、数列と数的推理に時間を使いましょう。
数列では以下のような問題が出題されます。
【例題】
次の数字はある規則性にしたがって並んでいる。空欄にあてはまる数字はどれか。
19、26、33、40、47、【 】、【 】
- 54、61
- 55、62
- 54、62
- 55、60
- 53、60
【解答&解説】
「後ろの数-前の数」を求めると、
- 26-19=7
- 33-26=7
- 40-33=7
- 47-40=7
なので、与えらえた数列は7ずつ増加していることがわかります。
よって、空欄は47+7=54、54+7=61なので、正解は1・・・(答)です。
SCOAで数列問題が出題された場合、まずは以下2つのどちらかを疑ってください。
- 等差数列
- 等比数列
等差数列は上記でご紹介した例題のように、同じ数ずつ増える数列のことです。
等差数列の例としては以下があげられます。
- 2、5、8、11、14、17・・・(2ずつ増える)
- 4、8、12、16、20・・・(4ずつ増える)
等比数列は同じ数ずつ掛け算される数列のことです。
等差数列の一例は以下です。
- 2、4、8、16、32・・・(2ずつ掛け算)
- 3、9、27、81、243・・・(3ずつ掛け算)
SCOAでは等差数列・等比数列以外にも、
- 足し算と掛け算が交互に登場する
- 足す数が1ずつ増えていく
といった数列も出題されますが、ベースとなっているのは等差数列と等比数列であることが多いので、SCOAを受検予定の人は等差数列と等比数列の違いをしっかりと理解しておきましょう。
また、SCOAの数列問題では稀に2進法を活用した問題が出題されるケースもあります。
2進法は0と1だけで表される記数法で、1の次は10に桁が繰り上がります。
※私たちが普段目にする数字(「100円」「5個」など)は10進法です。
例えば10進法の「1、2、3、4、5・・・」は2進法では「1、10、11、100、101・・・」となります。
では、2進法を使った数列の例題を1問ご紹介します。
【例題】
次の数字はある規則性にしたがって並んでいる。空欄にあてはまる数字はどれか。
11、101、111、1001、【 】、【 】、(2進法)
- 1011、1100
- 1011、1101
- 1010、1011
- 1100、1110
- 1100、1001
【解答&解説】
与えられた数列を10進法に変換すると、
- 11→3
- 101→5
- 111→7
- 1001→9
となります。つまり、与えられた数列は
3、5、7、9、【 】、【 】、(10進法)
となり、2ずつ増える等差数列なので、空欄にあてはまるのは11と13です。
11と13を2進法に変換すると、
- 11→1011
- 13→1101
になるので、正解は2・・・(答)となります。
2進法の数列については「SCOAの数列問題の例題と解き方のコツをわかりやすく解説」で詳しく解説しているので、ぜひご覧ください。
数的推理
数的推理では以下の3分野から問題が出題されます。
- 文章題
- 数の性質
- 図形
それぞれについて詳しく解説します。
文章題
文章題では濃度問題や速度算、損益算など幅広い分野から問題が出題されます。
以下を必ず覚えておきましょう。
- き・は・じの法則
- 溶液の濃度の公式
- 仕事算の解き方
- 旅人算の解き方
- 損益算の用語と解き方
それぞれの詳細は以下です。
【き・は・じの法則】

※速度算の詳細や練習問題を解きたい人はこちらの記事をご覧ください。
【溶液の濃度の公式】
濃度[%]=溶質の重さ / 溶液の重さ × 100=溶質の重さ / (溶質の重さ+溶媒の重さ) × 100
食塩水の場合、食塩が溶質、水が溶媒、食塩水が溶液に相当します。
※濃度算の詳細や練習問題を解きたい人はこちらの記事をご覧ください。
【仕事算の解き方】
仕事算とは、ある仕事を片付けるには何時間(何日)かかるかを求めたり、ある仕事を〇〇日までに終わらせるには1日あたりどれくらいの量をこなさなければならないかなどを求めたりする計算のことです。
※仕事算の詳細や練習問題を解きたい人はこちらの記事をご覧ください。
【旅人算の解き方】
旅人算とは2人の人間が出会ったりすれ違ったりするまでの時間や道のりなどを求める問題です。
※旅人算の詳細や練習問題を解きたい人はこちらの記事をご覧ください。
【損益算の用語と解き方】
損益算を解くためには以下4つの用語を必ず理解しておく必要があります。
- 原価(仕入れ値)
- 定価
- 売値
- 利益
それぞれの用語の詳細や損益算の練習問題を解きたい人はこちらの記事をご覧ください。
数の性質
数の性質では以下のような問題が出題されます。
【例題】
√5やπのような数を何と呼ぶか。
- 整数
- 自然数
- 素数
- 無理数
- 有理数
【答え】無理数
SCOAを受検予定の人は以下を必ず暗記しておいてください。
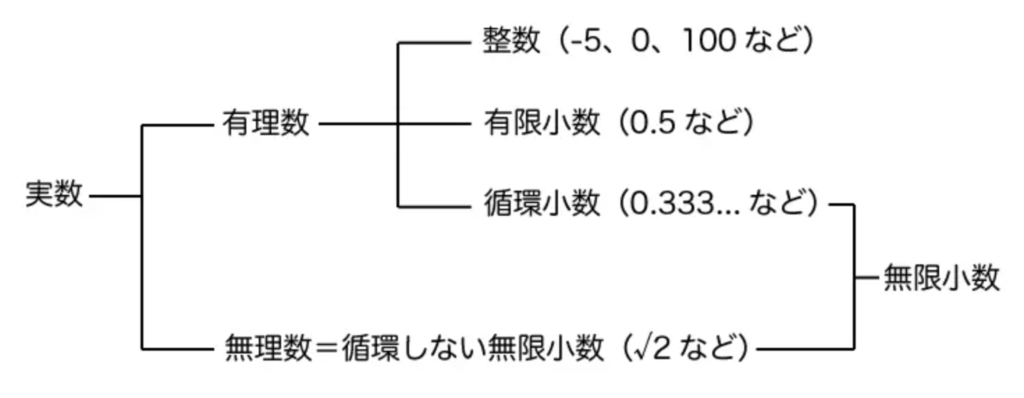
※上記の図の詳細はこちらの記事をご覧ください。
ちなみにですが、整数は
- 自然数(正の整数)
- 0
- 負の整数
に分けることができます。自然数(正の整数)の例は1、2、3、4・・・です。
負の整数の例は-1、-2、-3、-4・・・・です。
素数は1と自分自身以外の数では割り切れない数のことです。
素数の例としては3、5、7、11などがあげられます。1は素数ではないのでご注意ください。
図形
SCOAで出題される図形問題は一定の知識が必要がないと解けない問題が多いです。
SCOAを受検予定の就活生や転職活動中の社会人は以下11個の知識を必ず頭に入れておきましょう。
- 円周角と中心角
- 接弦定理
- 対頂角・同位角・錯角
- 多角形の外角の和と内角の和
- 三平方の定理
- 扇形の弧の長さ、扇形の面積
- 三角形の相似条件
- 座標平面上の2点間の距離
- 直方体の対角線
- 円錐の高さと体積
- 垂直な直線の方程式
それぞれの詳細は「SCOAの図形問題を例題で解説!暗記必須の11個の知識も図解でご紹介!」をご覧ください。
論理の対策方法
SCOAの論理では以下3つの問題が出題されます。
- サイコロ
- 推論
- 判断推理
SCOAの受検までに時間がない人は推論と判断推理を重点的に対策してください。
推論
推論は与えられた条件から推論(推理)して、誤りまたは断定できない結論を選ぶ問題です。
例題を1問ご紹介します。
【例題】
以下2つのことを前提として、推論ア〜オの中で、明らかに誤りであるものか、あるいは与えられた前提だけからでは、はっきりと断定できないものの記号を選び、その組み合わせを番号で答えなさい。
- AはBよりも小さい
- CはBよりも小さい
ア:Cが一番小さい
イ:AとCは等しい
ウ:Bが一番大きい
エ:BはCよりも大きい
オ:BはAよりも大きい
- ア、イ
- ウ、オ
- ア、エ
- イ、オ
- ア、ウ
【解答&解説】
まずは与えられた2つの条件を以下のように記号で表します。
- A<B
- C<B
以上より、AとCの大小関係は不明です。
アの「Cが一番小さい」ですが、一番小さいのはAかCかわからないので断定できません。
イの「AとCは等しい」ですが、上記の通りAとCの大小関係は不明なので断定できません。
よって、正解は1・・・(答)となります。
SCOAの推論のポイントは与えられた条件を記号や図にまとめて視覚的にわかりやすくすることです。
上記の例題では与えられた条件から記号(不等号)を使って以下のように表現しました。
- A<B
- C<B
上記の例題ではAとCの大小関係は不明でしたが、例えば、
- A>B
- B>C
の場合だと、A>B>Cが成り立つので、A・B・Cの大小関係がはっきりとします。
与えられた条件は頭の中だけで処理すると混乱しやすいので、SCOAを受検予定の就活生や転職活動中の社会人はまず、記号や図にまとめることを意識してください。
※詳しくは「SCOAの推論とは?解き方のポイントを例題でわかりやすく解説」をご覧ください。
判断推理
判断推理では以下2つの問題が頻出なので、必ず解き方を覚えください。
【例題1】
以下の図のような道があるとき、点Aを出発して点Bへ行く最短経路は何通りあるか。
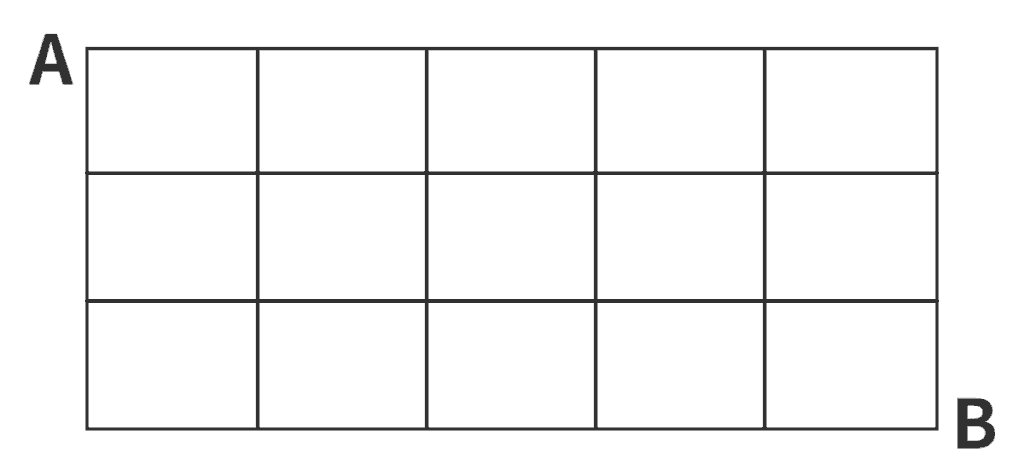
- 50通り
- 56通り
- 62通り
- 68通り
- 74通り
【解答&解説】
交差路またはT字路の間を1つの道として見ると、点Aから点Bに最短距離で行くためには、右に5つ、下に3つの合計8つの道を移動することになります。
よって、全部で8つの道から下に3つの道を選んだ組み合わせなので、組み合わせの公式を使って8C3=(8×7×6)/(3×2×1)=56[通り]・・・(答)となります。
【例題2】
円周上に等間隔に8個の点を取り、その中から3個の点を結んで三角形を作るとき、何個の三角形ができるか。
- 32個
- 44個
- 56個
- 68個
- 80個
【解答&解説】
以下の図のように、円周上に等間隔に8個の点A〜Hをとって考えます。
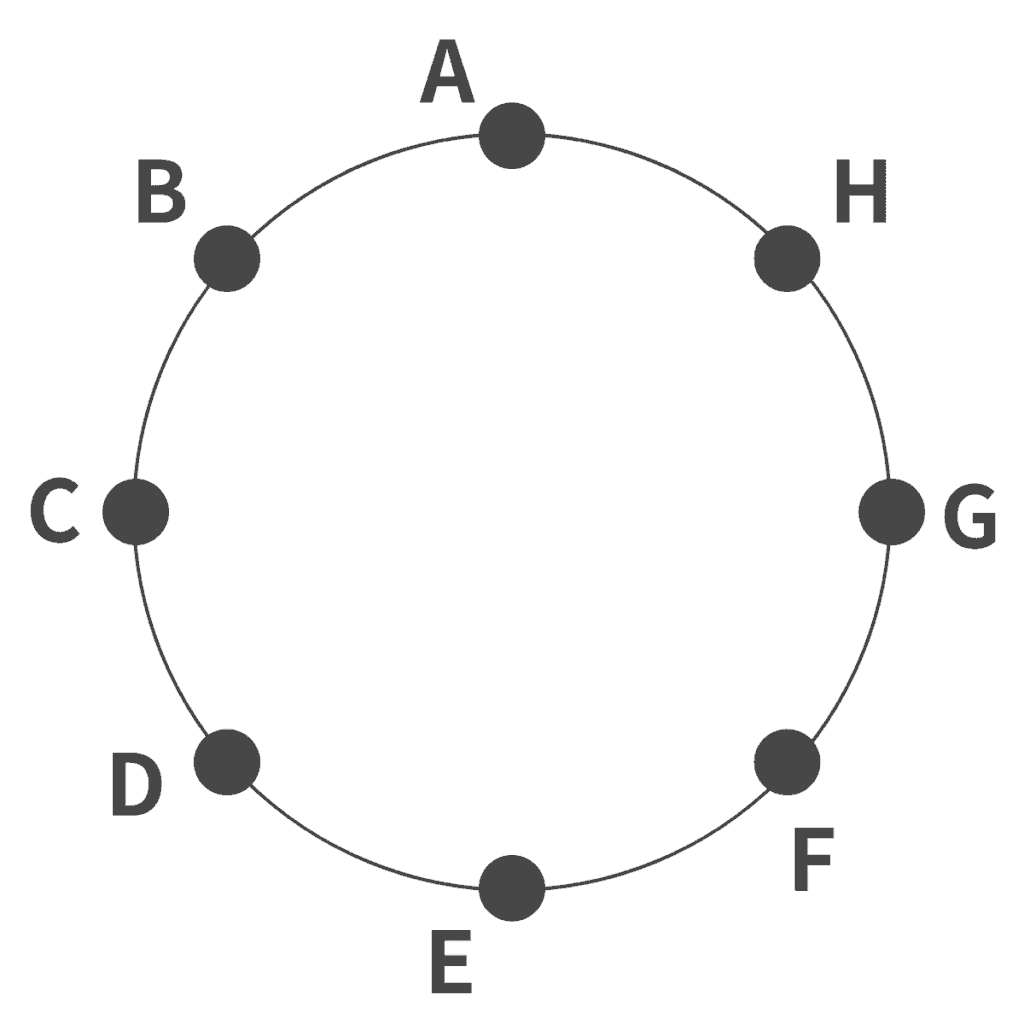
8個の点のうち3個の組み合わせで三角形を作ることができます。
よって、異なる8個のものから3個を選んだ組み合わせなので、組み合わせの公式を使って8C3=(8×7×6)/(3×2×1)=56[個]・・・(答)となります。
英語の対策方法
SCOAの英語で登場する英単語や英熟語は中学・高校で学習するレベルのものです。
なので、中学・高校レベルの英単語や英熟語のほとんどをすでに忘れてしまっている人がSCOAの英語の対策を行うのは正直言ってかなり厳しいです。
そんな人は英語を潔く捨てて、他の科目の対策に時間を費やすのも戦略としては十分ありです。
SCOAの英語では長文読解は出題されず、以下のような英単語・英熟語や文法問題が出題されます。
対策方法としてはSCOAの問題集を購入してできるだけ多くの英単語・英熟語を暗記するしかありません。
【例題1】
次の単語の意味として適切なものを選びなさい。
sensible
- impression
- showing good sense
- horrible
- happy accident
- neither good nor bad
【解答&解説】
正解は2・・・(答)です。
sensibleの意味は「分別のある、賢明な」です。
それぞれの選択肢の意味は以下の通りです。
- 印象
- 良識を示す
- 恐ろしい
- 幸運な偶然の出来事
- 可もなく不可もなく
【例題2】
次の文の空欄に入るものとして、適切なものは次のうちどれか。
He went out 【 】 the house at 8:00 AM.
- on
- by
- of
- at
- with
【解答&解説】
正解は3・・・(答)です。「go out of〜」で「〜から出る」という意味になります。
英文の日本語訳は「彼は午前8時にその家を出た」です。
※「SCOAの英語を完全解説!単語レベルや例題・対策方法は?」もぜひ合わせてご覧ください。
常識の対策方法
常識では社会と理科が10問ずつ出題されます。
社会は地理、歴史、公民から幅広く出題され、理科は生物、化学、地学、物理から幅広く出題されます。
まずは社会から解説します。
社会
社会はすべて以下のような知識問題なので、知ってるか知らないかがすべてです。
英語と同様にSCOAの問題集を購入してできるだけ多くの知識を暗記するしかありません。
SCOAの受検までに時間がない人は対策の優先順位は下げてください。
【例題】
オーストラリアの面積は約769万km2である。これは日本の面積の約何倍にあたるか。
- 約5倍
- 約15倍
- 約20倍
- 約40倍
- 約60倍
【解答&解説】
日本の面積は約38万km2です。
769÷38=20.23・・・より、正解は3・・・(答)です。
理科
生物と地学は社会と同じく知識問題が中心です。なので、SCOAの受検までに時間がない人は対策の優先順位は下げてください。
化学と物理は公式さえ知っていれば解ける問題もあります。
以下の公式は頻出なので、必ず覚えておいてください。
【オームの法則】
電流(A)=電圧(V)/抵抗(Ω)
【自由落下の速度と位置】
y=1/2 × gt2
y:落下距離[m]、g:重力加速度、t:球がに地面にまでの時間[秒]
【運動方程式】
F=ma
※物体に力を加えたとき、力の向きに加速度aを生じ、aは加えた力Fに比例し、物体の質量mに反比例する。
【ボイル・シャルルの法則】
一定量の気体の体積(V)は圧力(P)に反比例し、絶対温度(T)に比例する。
一定量の気体の初めの状態を(P1、T1、V1)、終わりの状態を(P2、T2、V2)とすると、
P1V1 / T1 = P2V2 / T2 = 一定
となります。
【仕事率の公式】
仕事率=仕事/時間
仕事=質量 × 9.8m/s2 × 高さ
※「SCOAで常識問題・時事問題は出るので対策必須!例題や対策方法を解説」と「SCOAの理科・社会・化学・地理の対策方法を例題でわかりやすく解説!」もぜひ参考にしてください。
SCOAの科目別の対策方法は以上となります。
SCOAの受検までに時間がない人は本記事でご紹介した公式や知識だけを覚えて本番に挑むようにしてください。