
SCOAでは判断推理という問題が出題されることがあります。
※「SCOA総合適性検査とは?対策方法や例題・試験の種類などを完全解説!」もぜひ参考にしてください。
後ほど詳しく解説しますが、判断推理は論理的な思考力が問われる数学の問題です。
本記事ではSCOAの受検回数=100回以上・日本で一番SCOAを熟知している私ナオトが、SCOAの判断推理とは何か・対策方法について例題を使いながら徹底解説していきます。
SCOAを受検予定の就活生や転職活動中の社会人はぜひ参考にしてください。
ちなみにですが、SCOAにはたった3時間の勉強でSCOAが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSCOA受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
SCOAの判断推理とは?
まず前提として、SCOAにはSCOA-AやSCOA-Fなど様々な種類があります。
※SCOAの種類の詳細は「SCOAは何問?100分で120問?SCOAの種類ごとに解説!」をご覧ください。
このうち、SCOA-AとSCOA-FとSCOA-iでは論理という科目が用意されています。
論理はその名の通り論理的な思考力を問う科目で、以下3つの分野から問題が出題されます。
- サイコロ
- 推論
- 判断推理
判断推理では
- 道順の組み合わせ
- 数値の予想
- 図形問題
- 時計問題
- 年齢算
- 集合
など、かなり幅広い分野から問題が出題されるので事前の勉強・対策は必須です。
🔽 本にも載ってない極秘情報 🔽
【SCOA】判断推理の問題例
本記事では上記でご紹介した6つの分野の問題例をご紹介します。
解答・解説も掲載しているので、SCOAを受検予定の就活生や転職活動中の社会人はぜひ解いてみてください。
※SCOAの問題をもっと解きたい人は「SCOA練習問題・例題124問無料!問題数日本一!言語・英語など全科目対応!」もぜひ合わせてご覧ください。
【例題(道順の組み合わせ)】
以下の図のような道があるとき、点Aを出発して点Bへ行く最短経路は何通りあるか。
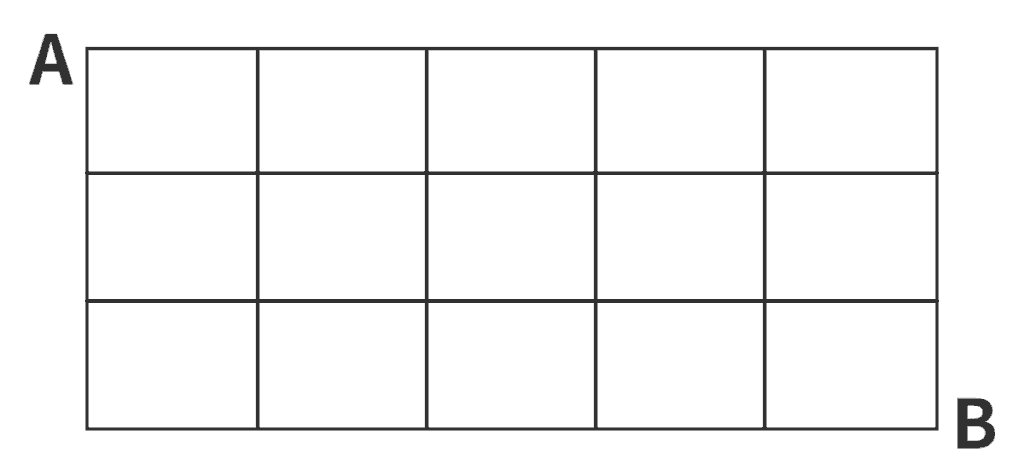
- 50通り
- 56通り
- 62通り
- 68通り
- 74通り
【解答&解説】
交差路またはT字路の間を1つの道として見ると、点Aから点Bに最短距離で行くためには、右に5つ、下に3つの合計8つの道を移動することになります。
よって、全部で8つの道から下に3つの道を選んだ組み合わせなので、組み合わせの公式を使って8C3=(8×7×6)/(3×2×1)=56[通り]・・・(答)となります。
【例題(数値の予想)】
1+1=2、2+2=6、3+3=12、4+4=20、5+5=30、6+6=42という計算が成り立つとすると、7+7はいくつになるか。
- 14
- 49
- 56
- 63
- 70
【解答&解説】
足し算の答えの部分が数列(2、6、12、20、30、42)になっていると考えます。
各数字の差に注目してみると、以下のようになっていることがわかります。
- 6-2=4
- 12-6=6
- 20-12=8
- 30-20=10
- 42-30=12
よって、42の次は42+14=56であることが推測できます。
以上より、正解は3・・・(答)となります。
※「SCOAの数列問題の例題と解き方のコツをわかりやすく解説」もぜひ参考にしてください。
【例題(図形問題)】
円周上に等間隔に8個の点を取り、その中から3個の点を結んで三角形を作るとき、何個の三角形ができるか。
- 32個
- 44個
- 56個
- 68個
- 80個
【解答&解説】
以下の図のように、円周上に等間隔に8個の点A〜Hをとって考えます。
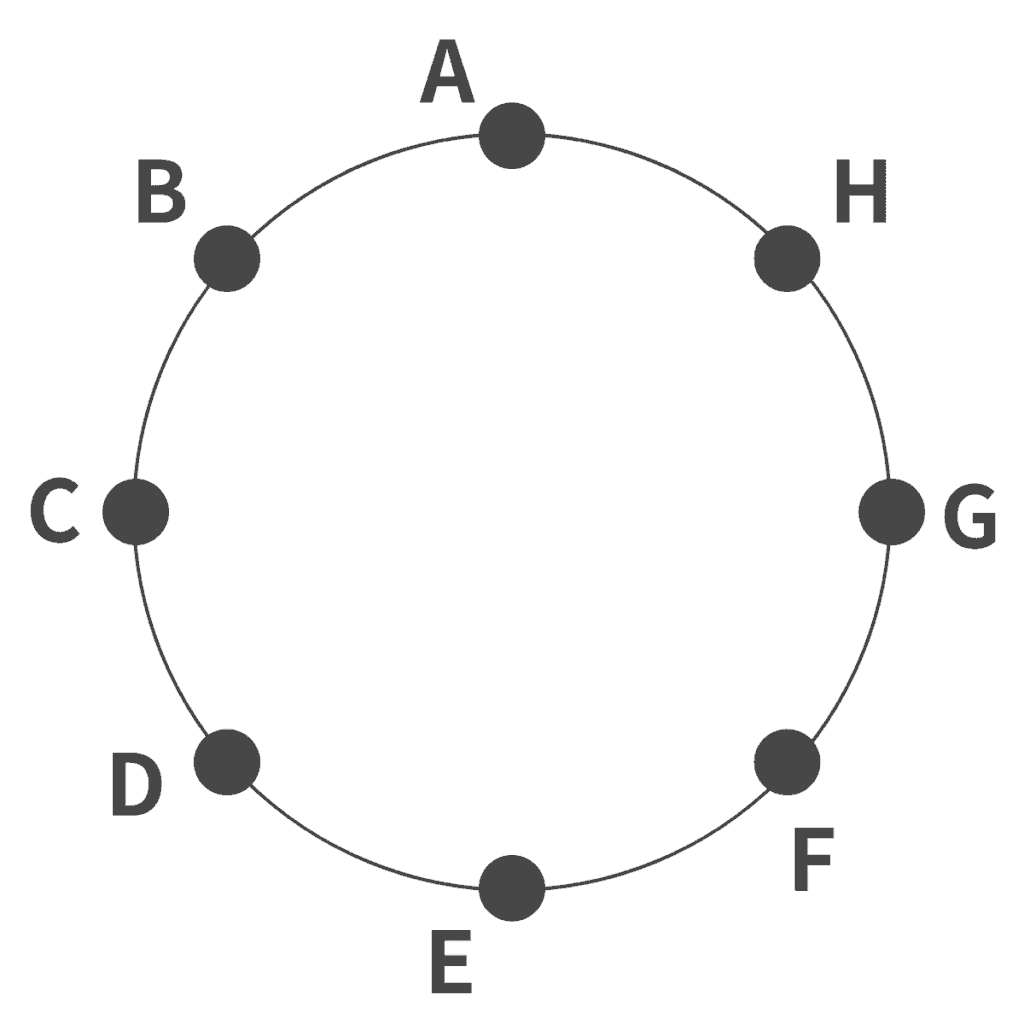
8個の点のうち3個の組み合わせで三角形を作ることができます。
よって、異なる8個のものから3個を選んだ組み合わせなので、組み合わせの公式を使って8C3=(8×7×6)/(3×2×1)=56[個]・・・(答)となります。
【例題(時計問題)】
東京とワシントンの時差は14時間である。4月1日16:30に東京を出発した飛行機が、18時間かかってワシントンに到着したとすると、その飛行機がワシントンに到着したときの現地時間は次のうちどれか。
- 4月2日20:30
- 4月2日10:30
- 4月1日20:30
- 4月2日22:30
- 4月1日23:30
【解答&解説】
東京とワシントンではワシントンのほうが遅く時間がめぐります。
時差が14時間ということは、東京の現地時間から14時間時計を戻すと、ワシントンの時間になります。
14時間時計を戻してから、飛行機の時間である18時間を足すと、到着時点でのワシントンの時間を求めることができます。
4月1日16:30から時計を14時間戻すと、4月1日2:30です。
4月1日2:30の18時間後は4月1日20:30なので、正解は3・・・(答)となります。
🔽 本にも載ってない極秘情報 🔽
【例題(年齢算)】
Sの3年後の年齢とTの18年前の年齢は等しい。また、現在のTの年齢と、Sの7年後の年齢を足すと60歳になる。現在、Tは何歳か。
- 39歳
- 33歳
- 41歳
- 37歳
- 35歳
【解答&解説】
SとTの現在の年齢をそれぞれS歳、T歳とおきます。
すると、以下の方程式を立てることができます。
- S+3=T-18
- T+S+7=60
2より、S=60-7-T=53-Tです。
これを1に代入すると、(53-T)+3=T-18となります。
整理すると、2T=74となるので、T=74÷2=37が求まります。
したがって、正解は4・・・(答)です。
【例題(集合)】
旅行に出かける120人に傘と帽子を持っていくか質問したところ、傘を持っていくと答えたのは67人、帽子を持っていくと答えたのは59人だった。また、傘も帽子も持っていかないと答えたのは36人だった。このとき、傘も帽子も持っていくと答えた人は何人か。
- 25人
- 42人
- 21人
- 31人
- 90人
【解答&解説】
以下のような表(カルノー表といいます)を作り、問題からわかる情報を記載していきます。
| 帽子を持っていく | 帽子を持っていかない | 計 | |
|---|---|---|---|
| 傘を持っていく | A | B | 67 |
| 傘を持っていかない | C | 36 | D |
| 計 | 59 | E | 120 |
求めるのはAです。
まずは、D=120-67=53であることがわかります。
よって、C=D-36=53-36=17となります。
したがって、A=59-C=59-17=42なので、正解は2・・・(答)です。
【SCOA】判断推理の対策方法
判断推理では上記でご紹介した道順の組み合わせと図形問題・年齢算が頻出なので、この3つの解き方は必ず頭に入れておきましょう。
※「SCOAの頻出問題・頻出英単語・頻出語句を一気にご紹介!」もぜひ参考にしてください。
特に年齢算は難易度がそこまで高くないので対策もしやすいです。
年齢算の解き方のコツですが、年齢の差は常に変わらないことに注目すると早く問題を解ける場合があります。
以下の例題を「年齢の差は常に変わらないこと」に注目して解いてみます。
【例題】
現在の父親の年齢は37歳で、子供の年齢は5歳である。父親の年齢が子供の年齢の2倍になるのは今から何年後か求めよ。
【解答&解説】
現在の父親と子供の年齢の差=37-5=32[歳]です。この年の差は何年経っても変わりません。
つまり、父親の年齢が子供の年齢の2倍になったとしても、年の差は32歳のままになります。
父親の年齢が子供の年齢の2倍になったときの子供の年齢=a[歳]とすると、そのときの父親の年齢は2a[歳]となります。
すると、2a-a=32が成り立つので、a=32[歳]となります。
現在の子供の年齢=5歳なので、正解は32-5=27[年後]・・・(答)となります。
年齢算において「年齢の差は常に変わらない」はかなり便利なテクニックとして使えるので、ぜひマスターしておきましょう。
🔽 本にも載ってない極秘情報 🔽
今回はSCOAの判断推理を取り上げました。
判断推理は出題範囲が広く対策がしづらいですが、SCOAの受検までに時間がない人は道順の組み合わせ・図形問題・年齢算を重点的に対策しましょう。


