SCOAの図形問題を例題で解説！暗記必須の11個の知識も図解でご紹介！

SCOAの数理では図形問題が出題範囲に含まれています。

※「SCOA総合適性検査とは？対策方法や例題・試験の種類などを完全解説！」もぜひ参考にしてください。

SCOAで出題される図形問題を解くには中学・高校で学習した知識が必要なので、その知識を覚えていないと解くことができません。

本記事ではSCOAを今までに100回以上受検してきたSCOAマスターの私ナオトが、SCOAの図形問題を例題でわかりやすく解説していきます。

SCOA受検者が必ず覚えておくべき図形に関する11個の知識も図解でご紹介するので、ぜひ最後までご覧ください。

ちなみにですが、SCOAにはたった3時間の勉強でSCOAが通過してしまう勉強法があります。

これさえあれば限りなく少ない努力で内定に大きく近づきます。

これは私が100回以上ものSCOA受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。

興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。

SCOAの図形問題を例題で解説！

SCOAの数理では以下のような図形問題が出題されます。

※「SCOA練習問題・例題124問無料！問題数日本一！言語・英語など全科目対応！」もぜひ合わせてご覧ください。

【例題】

以下の図において、∠ADC＝40°のとき、∠BACの大きさは何度か。

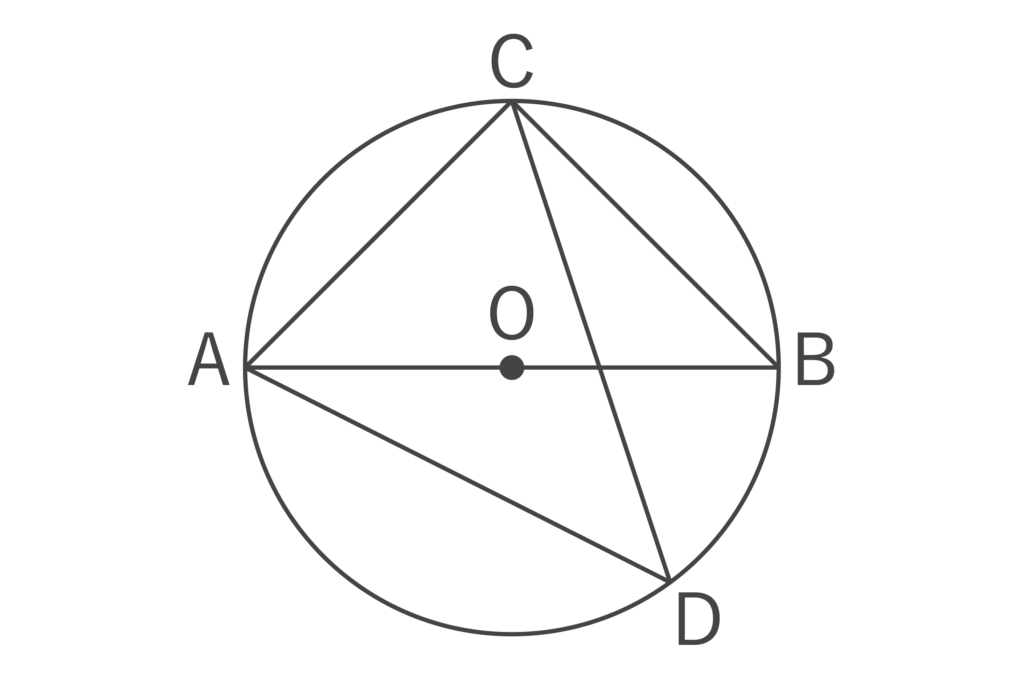
• 40°
• 45°
• 50°
• 55°
• 60°

【解答＆解説】

同じ弧に対する円周角は等しいので、∠ADC＝∠ABC＝40°が成り立ちます。

また、ABは円の直径なので、∠ACB＝180°÷2＝90°です。

よって、∠BAC＝180°-（∠ABC＋∠ACB）＝180°-（40°＋90°）＝50°・・・（答）となります。

🔽 本にも載ってない極秘情報 🔽

SCOAの図形で暗記必須の11個の知識

上記の例題の通り、SCOAで出題される図形問題は「同じ弧に対する円周角は等しい」などの一定の知識が必要であるケースが多いです。

SCOAを受検予定の就活生や転職活動中の社会人は以下11個の知識を必ず頭に入れておきましょう。

1. 円周角と中心角
2. 接弦定理
3. 対頂角・同位角・錯角
4. 多角形の外角の和と内角の和
5. 三平方の定理
6. 扇形の弧の長さ、扇形の面積
7. 三角形の相似条件
8. 座標平面上の2点間の距離
9. 直方体の対角線
10. 円錐の高さと体積
11. 垂直な直線の方程式

それぞれ詳しく解説していきます。

1：円周角と中心角

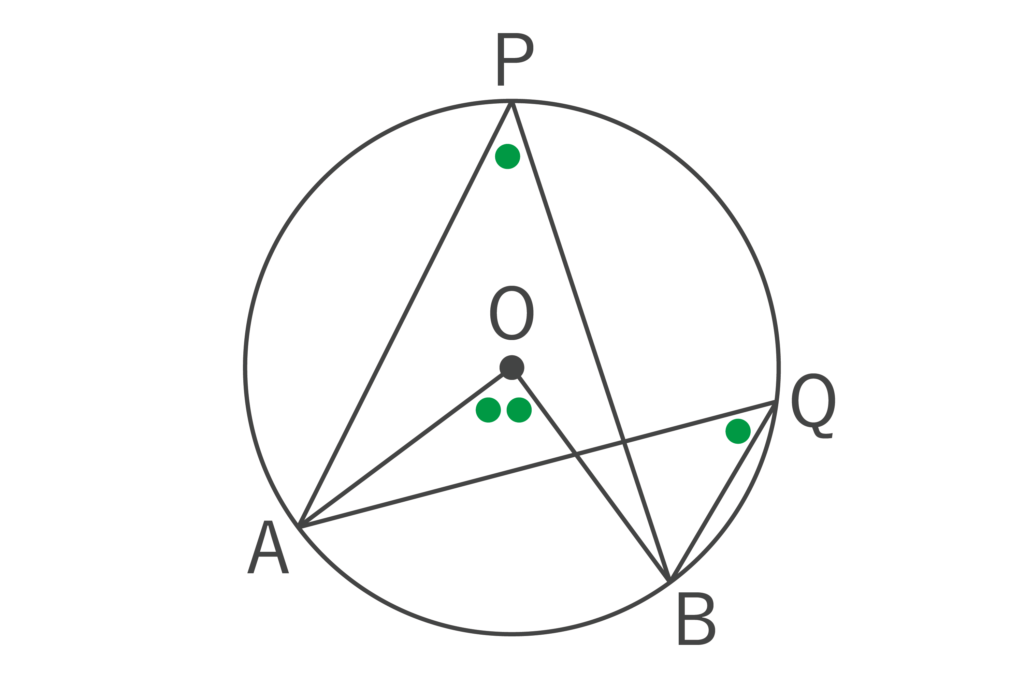
以下の図における∠APBを弧ABに対する円周角といいます。

また、∠AOBを弧ABに対する中心角といいます。

円周角の大きさは、中心角の大きさの1/2であり、同じ弧に対する円周角の大きさは等しくなります。

よって、∠APB＝∠AQBが成り立ちます。

2：接弦定理

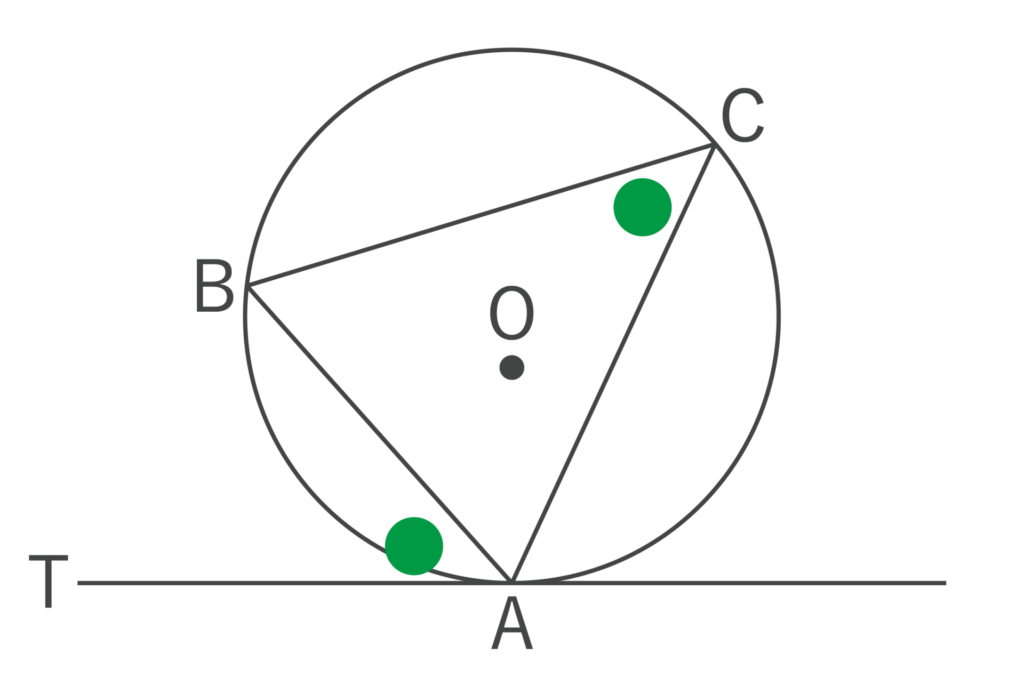
円周上の1点から引いた接線と接点を通る弦とのつくる角（以下の図では∠BAT）は、その角内にある弧に対する円周角（以下の図では∠ACB）に等しくなります（∠BAT＝∠ACB）

3：対頂角・同位角・錯角

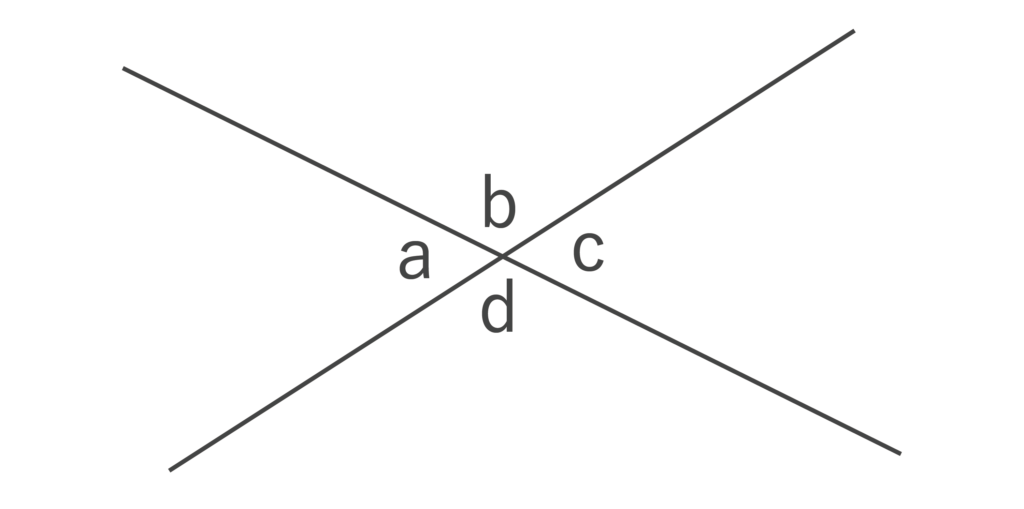
対頂角とは、以下の図のような位置関係にある2つの角のことです。

対頂角は等しいので∠a＝∠c、∠b＝∠dが成り立ちます。

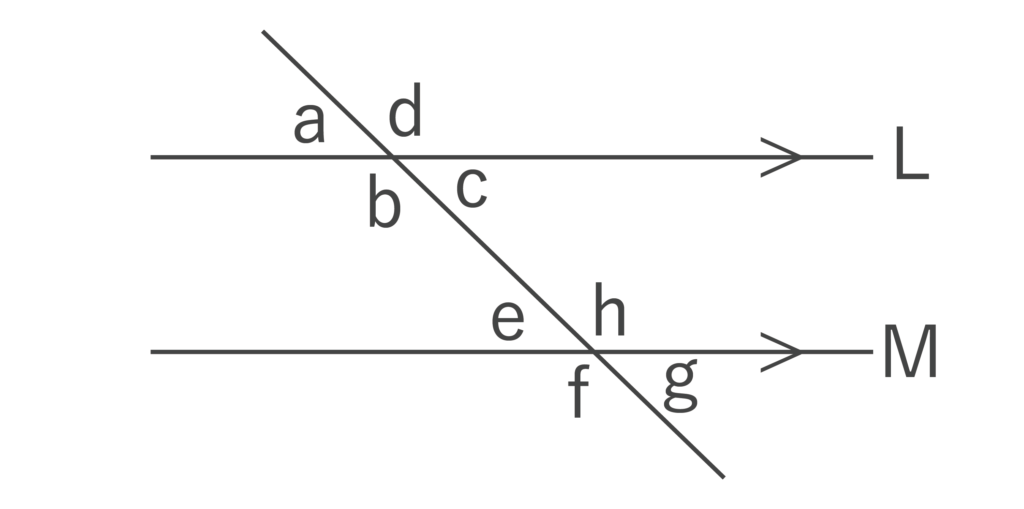
同位角とは以下の図において、∠aと∠e、∠bと∠fのような位置関係にある2つの角のことです。

また、錯角とは以下の図において∠bと∠h、∠cと∠eのような位置関係にある2つの角のことです。

以下の図のようにL//Mのとき、同位角は等しいものとなり、錯角も等しいものとなります。

4：多角形の外角の和と内角の和

多角形とは3本以上の線分によって囲まれた平面図形のことで、三角形・四角形・五角形・・・などの総称です（今回は五角形を例にして解説します）

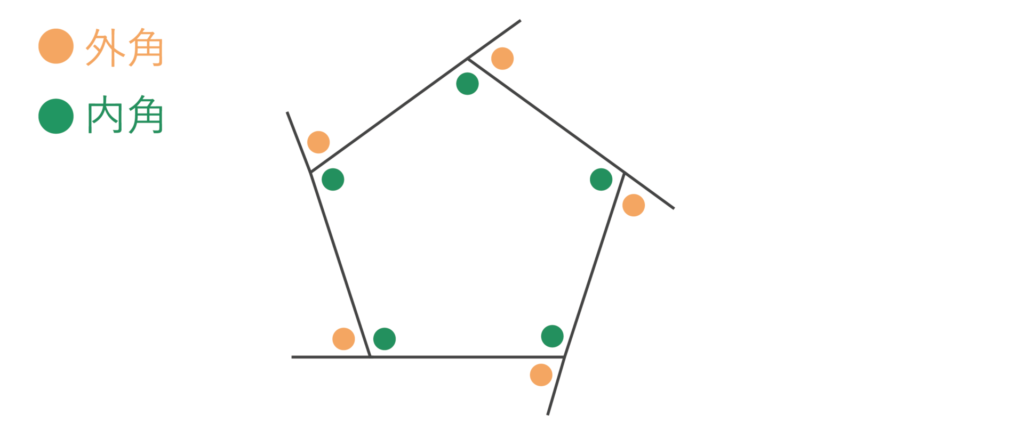
外角とは多角形の一辺とそれに隣り合う辺の延長線が成す角のことです。以下の図でいうと緑色の丸が外角に相当します。

内角とは隣り合う2辺からなる多角形の内側を向いた角度のことです。以下の図でいうとオレンジ色の丸が外角に相当します。

n角形においては以下の2つが成り立ちます。

• 外角の和＝360°
• 内角の和＝180°×（n-2）

例えば、五角形の内角の和は180°×（5-2）＝180° × 3＝540°となります。

十角形の内角の和は180°×（10-2）＝180°×8＝1440°となります。

🔽 本にも載ってない極秘情報 🔽

5：三平方の定理

以下の図のように、直角三角形の直角を挟む2辺の辺の長さをa、bとし、斜辺をcとすると、a²＋b²＝c²が成り立ちます。

これを三平方の定理といいます。

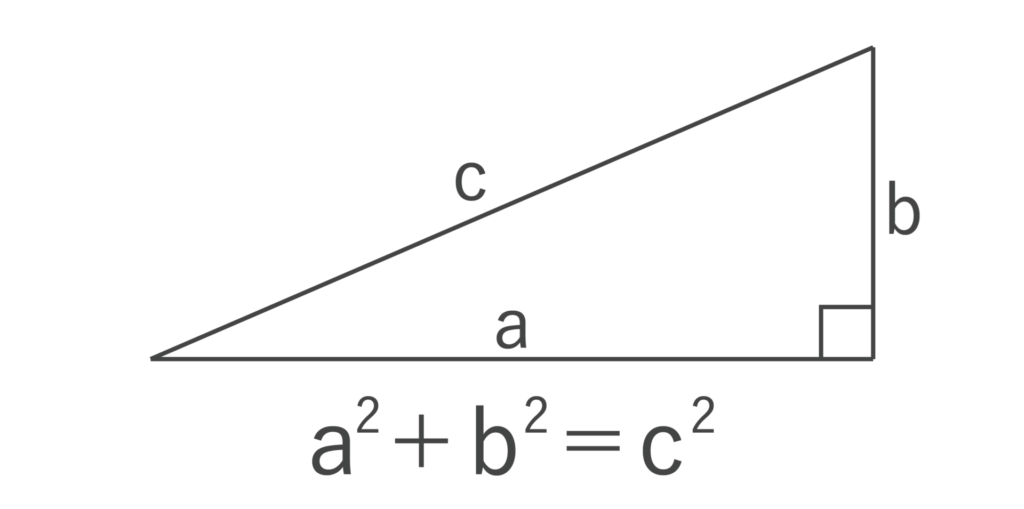
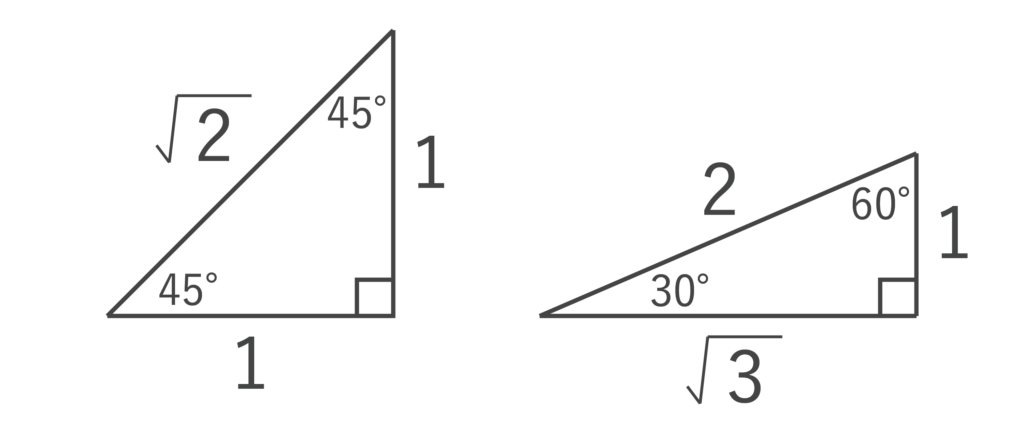
また、以下の図のような特別な直角三角形の3辺の比は1：1：√2、1：2：√3になっています。

6：扇形の弧の長さ、扇形の面積

半径＝r、中心角x°の扇形の弧の長さLは2πr × x/360となります。

また、面積SはL/2 × rとなります。

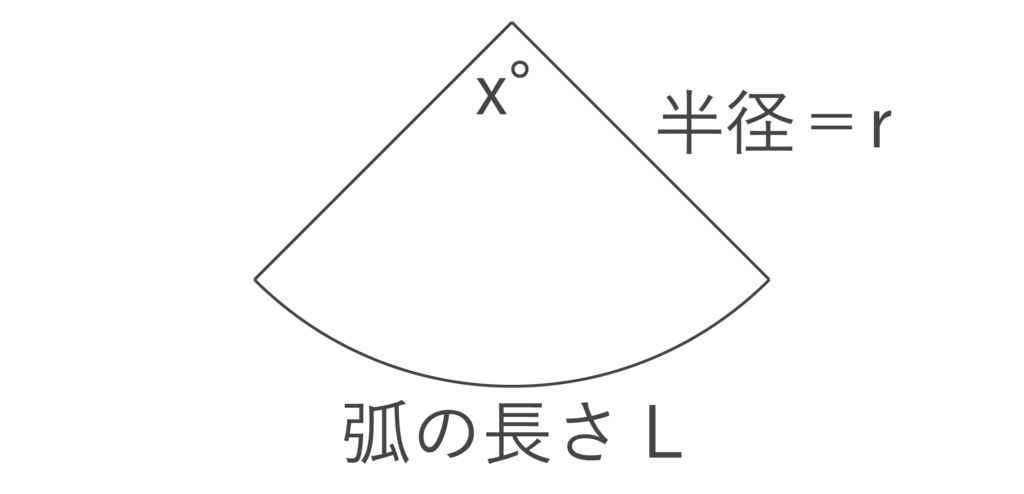
例えば、半径＝12cm、中心角60°の扇形の弧の長さは2π × 12 × 60/360 ＝24π × 1/6 ＝ 4π[cm]となります。

また、面積＝4π/2 × 12＝24π[cm²]となります。

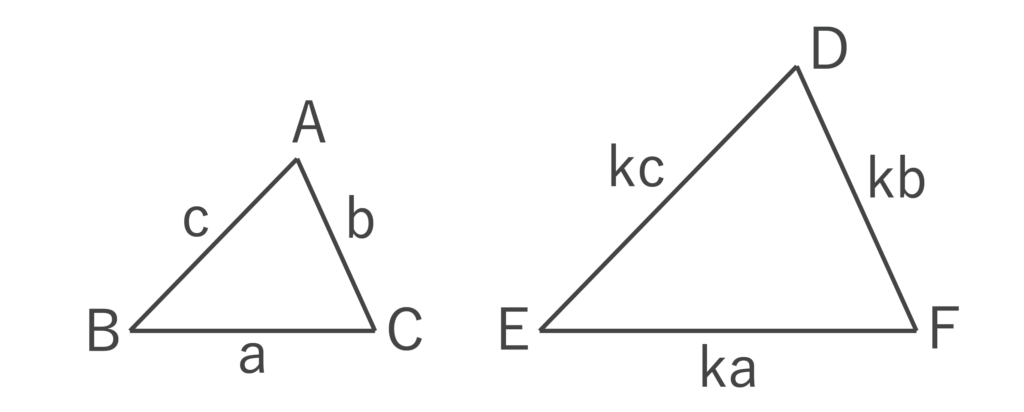
7：三角形の相似条件

2つの図形が縮小または拡大の関係になっているとき、「2つの図形は相似である」といいます。

2つの三角形が相似になるための条件は以下の3つです（どれか1つでもあてはまれば相似になります）

• 3組の辺の比が等しい
• 2組の辺の比が等しく、その間の角が等しい
• 2組の角がそれぞれ等しい

8：座標平面上の2点間の距離

xy平面上に（x₁、y₁）と（x₂、y₂）があるとき、この2点間の距離dは以下のようになります。

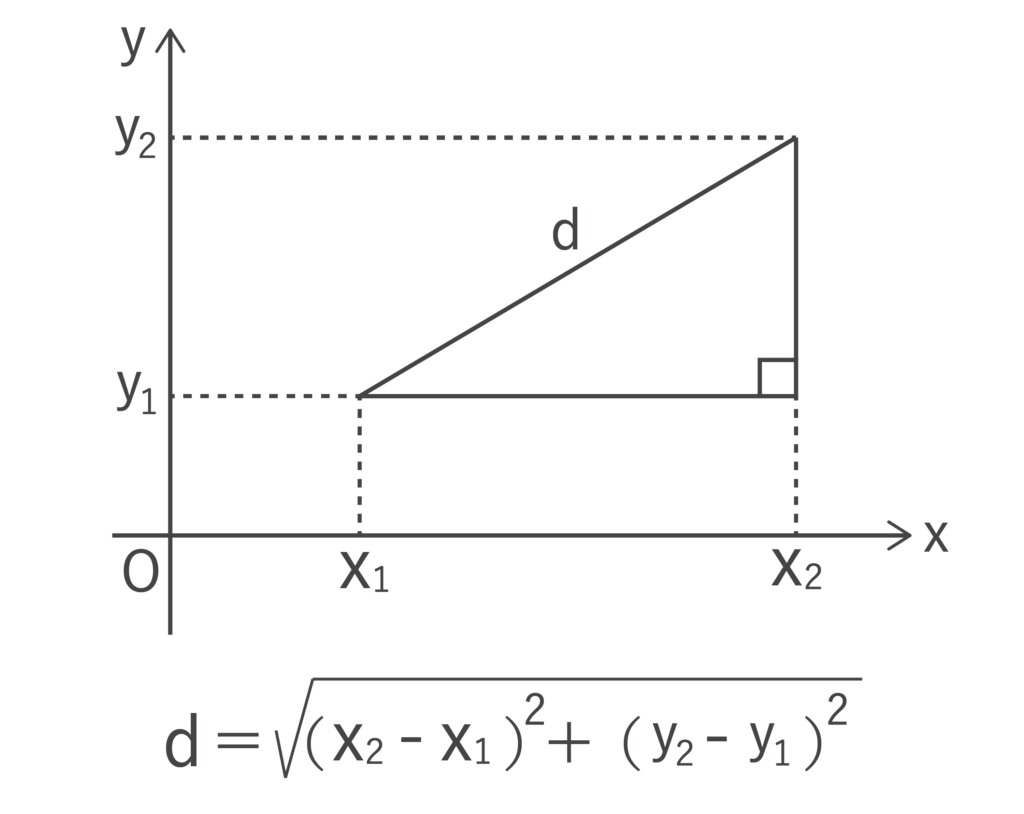
例えば、点（5、3）と点（10、7）の距離は（10-5）²＋（7-3）²＝25＋16＝41より、√41となります。

🔽 本にも載ってない極秘情報 🔽

9：直方体の対角線

以下の図のように縦がa、横がb、高さがcの直方体の対角線の長さPQは以下のようになります。

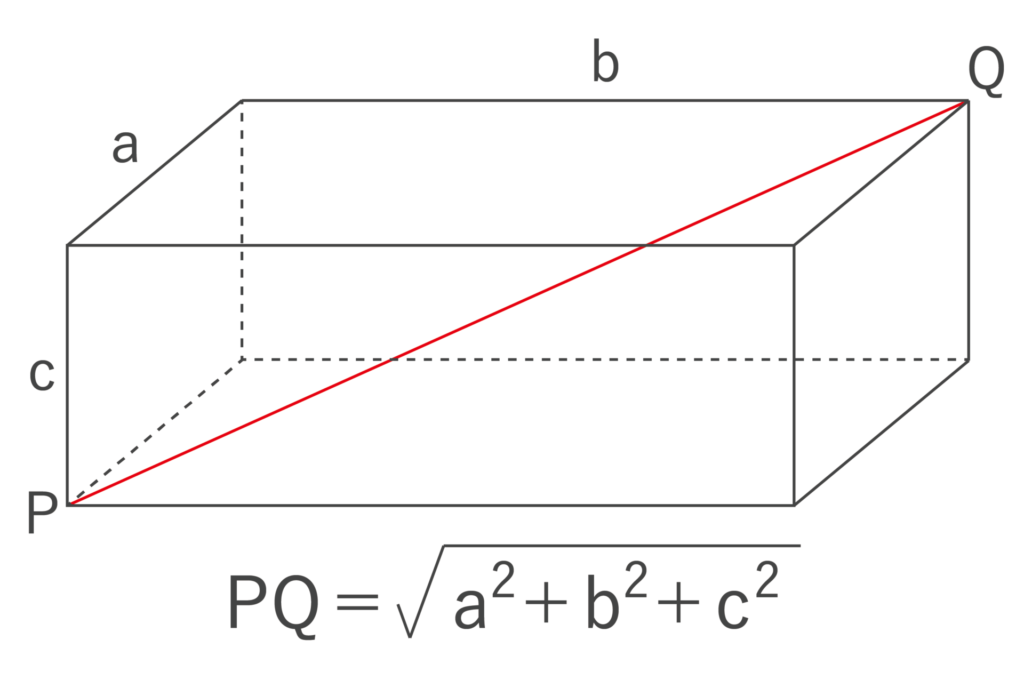
例えば、a＝3、b＝8、c＝5の場合、a²＋b²＋c²＝9＋64＋25＝98より、PQ＝√98＝7√2となります。

10：円錐の高さと体積

底面の半径がR、母線の長さがLの円錐の高さHと円錐の体積Vは以下のようになります。

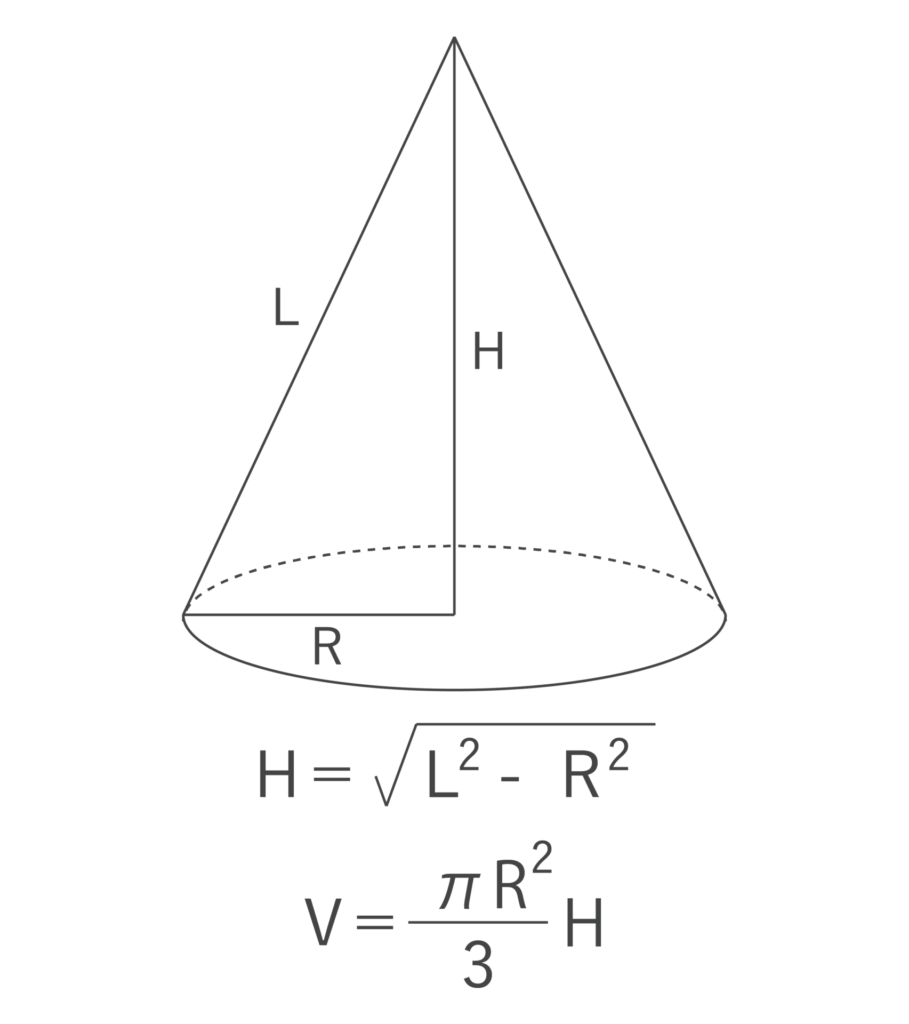
例えば、R＝3、L＝5の場合、L²-R²＝25-9＝16より、H＝4となります。

このときのV＝（π×3²）/3 × 4＝3π × 4＝12πとなります。

11：垂直な直線の方程式

xy平面において、y＝ax＋bとy＝cd＋dが垂直に交わるとき、ac＝-1となります。

ちなみにですが、a＝cのとき、y＝ax＋bとy＝cd＋dは平行になります。

以上を知っていると、以下の問題を解くことができます。

【例題】

点（3、-2）を通り、直線y＝3x＋5に垂直な直線の方程式は、次のうちどれか。

• y＝x/3＋5
• y＝x/3＋7
• y＝-x/3＋5
• y＝-x/3＋7
• y＝-x/3-1

【解答＆解説】

直線y＝3x＋5に垂直な直線の方程式なので、答えはy＝-x/3＋dの形になることがわかります。

y＝-x/3＋dは点（3、-2）を通るので、x＝3、y＝-2をy＝-x/3＋dに代入して、-2＝-1＋dとなります。

よって、d＝-1が求まります。

以上より、答えはy＝-x/3-1・・・（答）となります。

SCOA：図形の練習問題

最後に、SCOAで出題される問題の難易度に近い図形の練習問題を2問ご用意しました。

上記でご紹介した知識を使えば必ず解けるので、SCOAを受検予定の就活生や転職活動中の社会人はぜひ解いてみてください。

【練習問題1】

1つの外角が24°の正多角形は、正何角形か。

• 正八角形
• 正十五角形
• 正十二角形
• 正二十四角形
• 正十七角形

【解答＆解説】

上記でも解説した通り、n角形の外角の和は常に360°です。

360÷24＝15なので、正解は正十五角形・・・（答）となります。

【練習問題2】

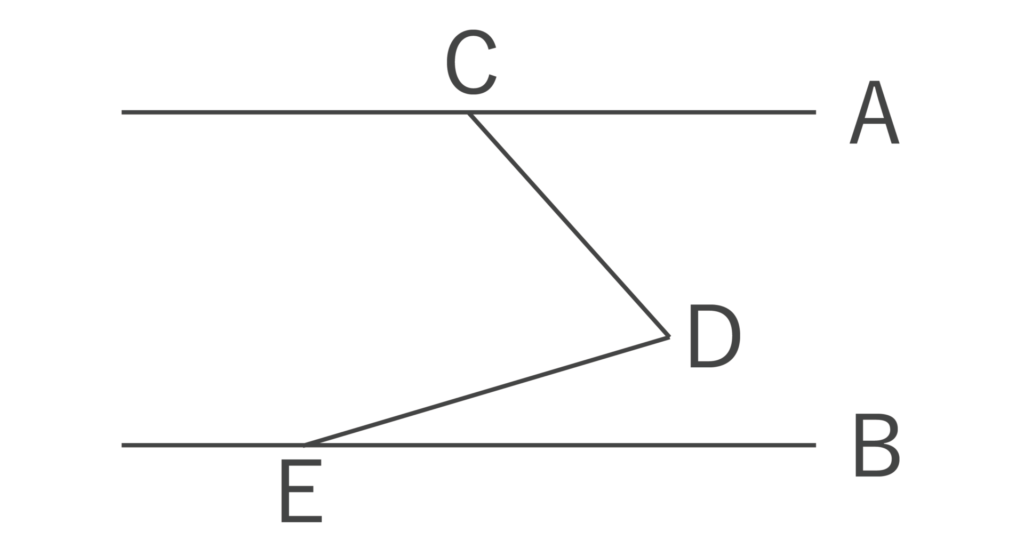
以下の図においてAとBは並行で、∠ACD＝58°、∠BED＝23°である。このとき、∠CDEの大きさを求めよ。

• 99°
• 58°
• 79°
• 23°
• 81°

【解答＆解説】

以下のように点Dを通り、AとBに並行な直線Fを引きます。

錯角は等しいので、

• オレンジ色の角度同士
• 緑色の角度同士

の大きさは等しくなります。

よって、∠CDE＝∠ACD＋∠BED＝58°＋23°＝81°・・・（答）となります。

🔽 本にも載ってない極秘情報 🔽

今回はSCOAの図形問題をご紹介しました。

図形問題は知識さえ知っていれば解ける問題が多いので、本記事でご紹介した11個の知識は必ず覚えておきましょう。