
適性検査の一種であるSCOAの論理という科目では空間把握に関する問題が出題されることがあります。
※「SCOA総合適性検査とは?対策方法や例題・試験の種類などを完全解説!」もぜひ参考にしてください。
後ほど詳しく解説しますが、空間把握では展開図の組み立てや立体の切断などに関する問題が出題されます。
今回はSCOAを今までに100回以上受検してきたSCOAマスターの私ナオトが、SCOAの空間把握について例題を使いながらわかりやすく解説していきます。
SCOAを受検予定の就活生や転職活動中の社会人はぜひ参考にしてください。
ちなみにですが、SCOAにはたった3時間の勉強でSCOAが通過してしまう勉強法があります。
これさえあれば限りなく少ない努力で内定に大きく近づきます。
これは私が100回以上ものSCOA受検を通して生み出した、どの本にも載っていない超コスパの良い究極の勉強法です。
興味のある人はぜひ以下のボタンからその方法をチェックしてみてください。
SCOAの空間把握とは?例題で解き方をわかりやすく解説
冒頭でも解説した通り、空間把握はSCOAの論理という科目で出題されます。
論理では
- サイコロ
- 推論
- 判断推理
という3つの問題が出題されますが、空間把握は判断推理で出題されます。
※サイコロ問題の詳細は「SCOAのサイコロ問題とは?解き方のコツを図解で徹底解説!」をご覧ください。
SCOAの空間把握では展開図の組み立てと立体の切断に関する問題が頻出なので、本記事ではその2つの例題をご紹介します。
※「SCOA練習問題・例題124問無料!問題数日本一!言語・英語など全科目対応!」もぜひ合わせてご覧ください。
【例題(展開図の組み立て)】
次の正八面体の展開図を組み立てたとき、辺BDと一致する辺はどれか。
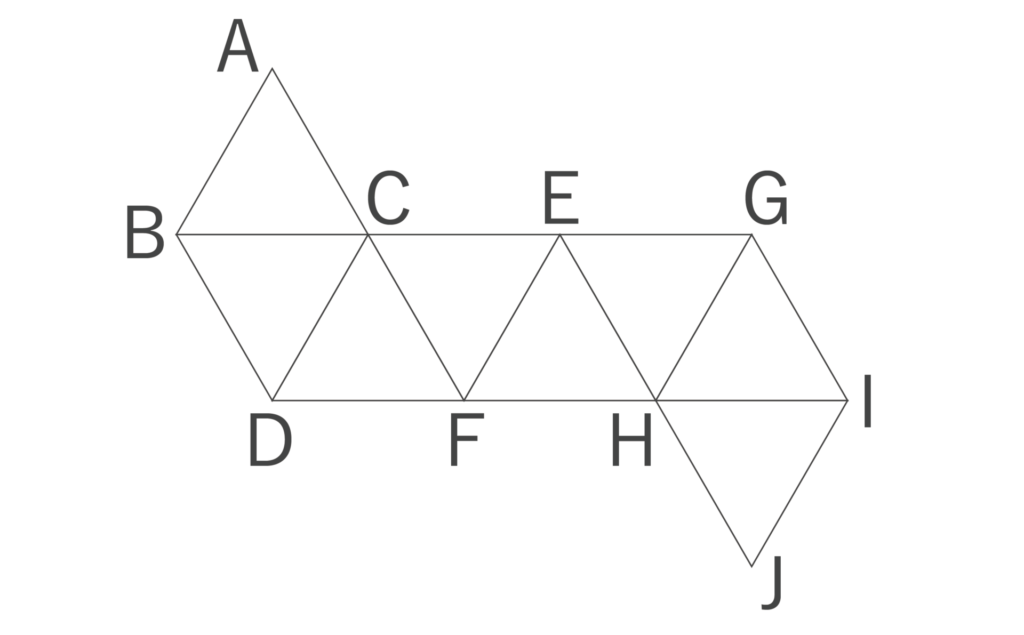
- GH
- GI
- HI
- HJ
- IJ
【解答&解説】
AF法(後ほど解説します)を使うと、以下の図のようになります。
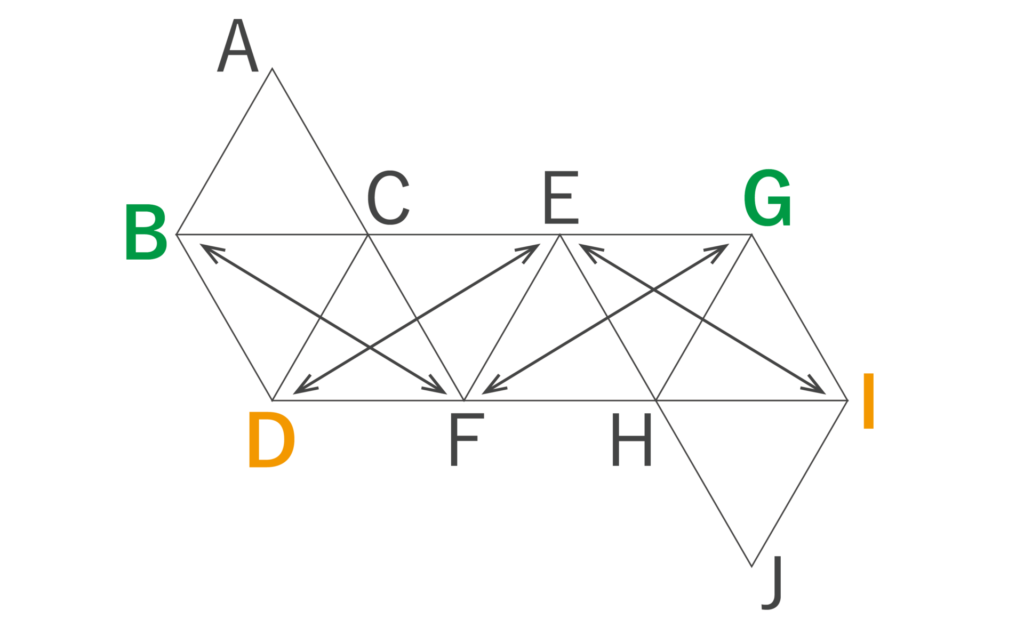
点Bについては、B↔F、F↔Gと展開できるので、B=Gとなります。
点Dについては、D↔E、E↔Iと展開できるので、D=Iとなります。
したがって、辺BDと一致するのは辺GIとなるので、正解は2・・・(答)です。
🔽 本にも載ってない極秘情報 🔽
【例題(立体の切断)】
図のような立方体を、辺AEの中点P、点B、辺EHの中点Qの3点を通る平面で切断するとき、切断面の図形はどれか。
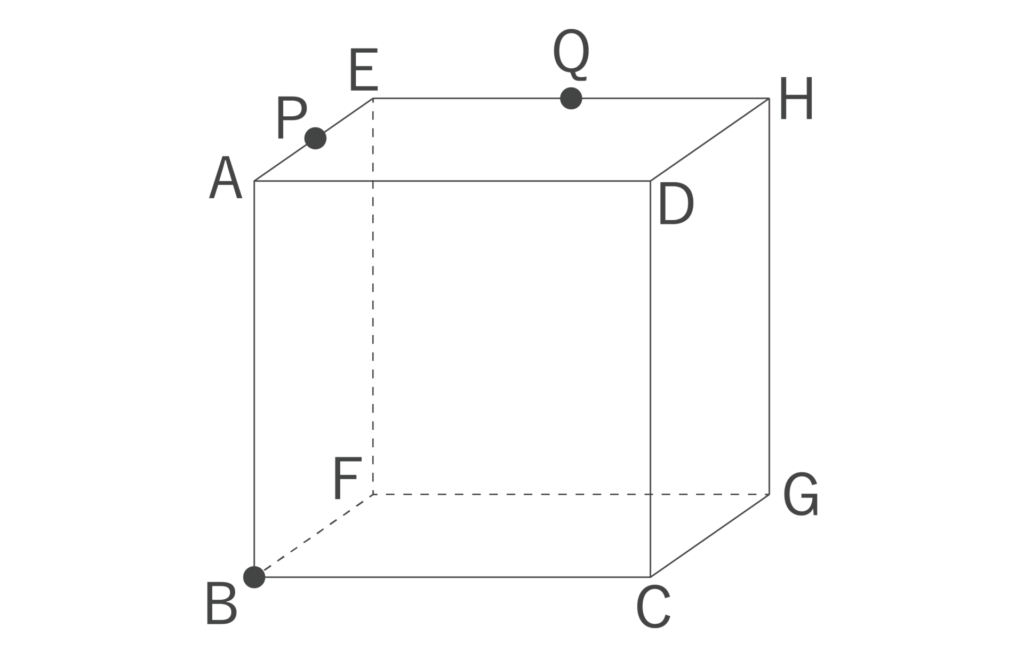
- 二等辺三角形
- 直角三角形
- 台形
- 長方形
- 正方形
【解答&解説】
立方体の切断は、以下3つの手順で行います。
- 同一平面上の点を結ぶ
- 平行な面にできる線は平行に描く
- 1と2でできなければ線を延長して角を作る
まず、1より、BとP、PとQは同一平面上なので結びます。一方、BとQは結べません。
2より、面ADHEと平行な面にあるPQと平行な線を、面BCGFの点Bから引きます。
立方体を真上から見ると下右図のようになるので、PQと平行な線はBGとなります。
最後に、また1より、GQを結びます。
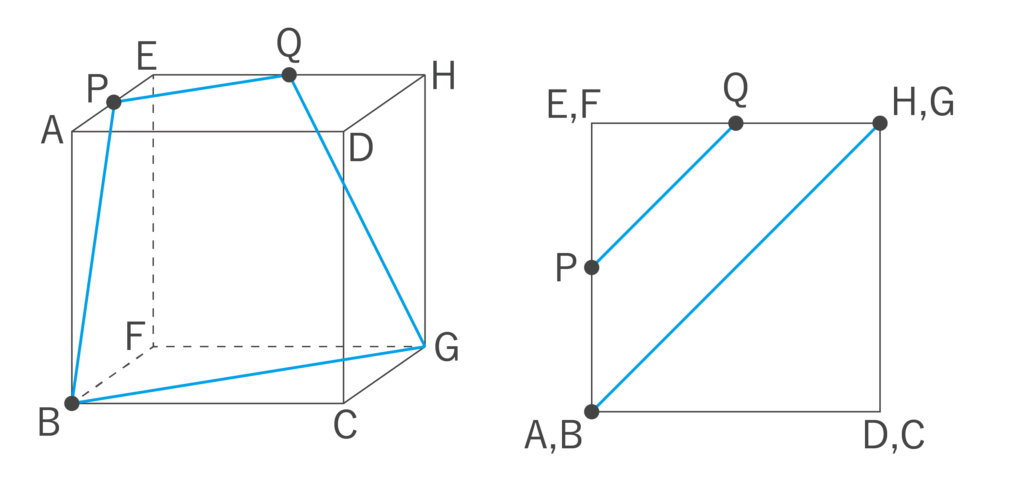
切断面は上左図のようになり、辺PQとBGだけが平行なので、できる図形は台形となります。
つまり、正解は3・・・(答)です。
SCOAの空間把握のポイント
上記でもご紹介しましたが、展開図の組み立て問題を解く際にはAF法が便利なので、SCOAを受検予定の就活生や転職活動中の社会人は覚えておきましょう。
以下の図のように、正八面体の6つの頂点をA〜Fとします。
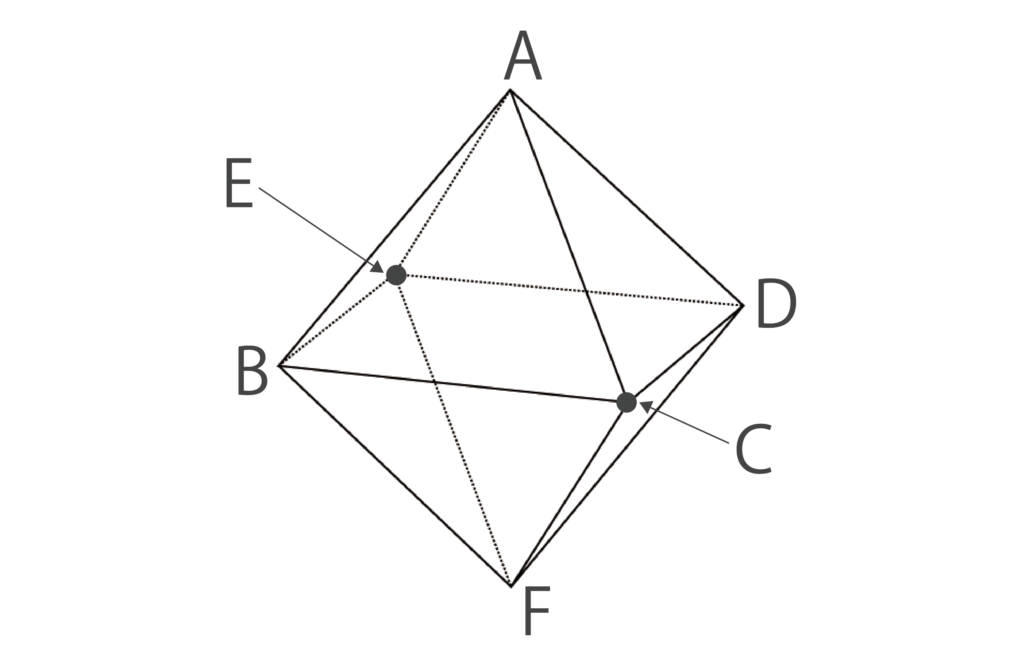
次に、以下の図のように
- A↔F
- B↔D
- C↔E
の3組の頂点のペアを作ります。
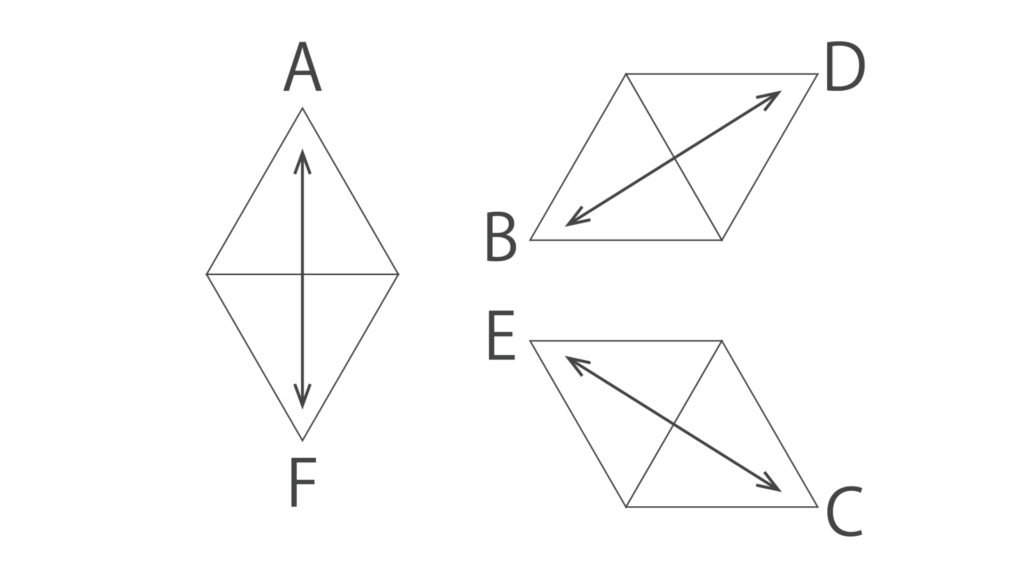
すると、これらの3組の位置関係は以下の図のようになります。
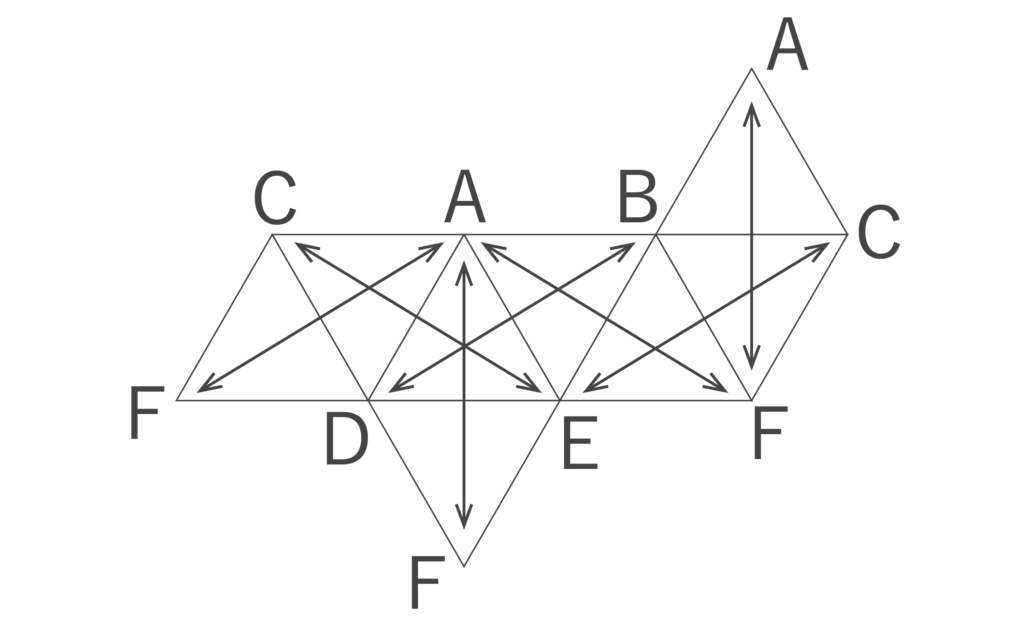
AF法は特に正八面体の展開図の問題を解く際に便利です。
ちなみにですが、正八面体に関する問題はTG-WEBでも頻出です。
TG-WEBで出題される正八面体に関する問題の例題を知りたい人は「正八面体の展開図はTG-WEBで頻出なので必ず暗記!11種類を一覧で紹介」をご覧ください。
🔽 本にも載ってない極秘情報 🔽
今回はSCOAの空間把握を取り上げました。
空間把握はそこまで難易度は高くないので、確実に得点できるようにしておきましょう。


